Let me begin with some excerpts that explain in broad terms what Kill Math is about:
When most people speak of Math, what they have in mind is more its mechanism than its essence. This "Math" consists of assigning meaning to a set of symbols, blindly shuffling around those symbols, and then interpreting meaning from the shuffled result...
This mechanism of math evolved for a reason: it was the most efficient means of modeling quantitative systems given the constraints of pencil and paper. Unfortunately, most people are not comfortable with bundling up meaning into abstract symbols and making them dance. Thus, the power of math beyond arithmetic is generally reserved for a clergy of scientists and engineers...
We are no longer constrained by pencil and paper. The symbolic shuffle should no longer be taken for granted as the fundamental mechanism for understanding quantity and change. Math needs a new interface...
Kill Math is my umbrella project for techniques that enable people to model and solve meaningful problems of quantity using concrete representations and intuition-guided exploration. In the long term, I hope to develop a widely-usable, insight-generating alternative to symbolic math...
A person should not be manually shuffling symbols [with pencil and paper]. That should be done, at best, entirely by software, and at least, by interactively guiding the software, like playing a sliding puzzle game. And, more contentiously, I believe that a person should not have to imagine the interpretation of abstract symbols. Instead, dynamic graphs, diagrams, visual models, and visual effects should provide visceral representations. Relationships between values, exponential blow-ups and negligible terms, should be plainly seen, not imagined...
In his talk Media For Thinking the Unthinkable Victor states a related but even more ambitious program. He quotes Richard Hamming's essay on The Unreasonable Effectiveness of Mathematics:
Just as there are odors that dogs can smell and we cannot, as well as sounds that dogs can hear and we cannot, so too there are wavelengths of light we cannot see and flavors we cannot taste. Why then, given our brains [are] wired the way they are, does the remark "Perhaps there are thoughts we cannot think," surprise you? Evolution, so far, may possibly have blocked us from being able to think in some directions; there could be unthinkable thoughts** Quantum mechanics is famously difficult to understand. This is due in part to unresolved conceptual problems in the foundations, which make it fair to say that no-one in the world really understands quantum mechanics. I have wondered for many years if the principal difficulty is that our brains aren't wired the right way. To recast this in Hamming's terms, perhaps quantum mechanics only appears difficult, but is actually easy to understand, provided one can think "thoughts we cannot think". Note that I'm not saying that the trouble is merely that we're missing some key theoretical idea or set of ideas. That's the point of view usually taken by people who worry about the foundations of quantum mechanics. Rather, perhaps we need to expand the class of thoughts we can think in some much more radical way. An argument for this point of view is that our brains evolved to understand a classical world. Such brains might perhaps come very poorly equipped to grasp a theory such as quantum mechanics, which doesn't obey principles as fundamental as local realism.
With that said, let me add the caveat that I believe the conventional point of view is likely correct, and we simply have not yet found a good conventional explanation of quantum mechanics, the type of explanation which could have been understood with some work by a physicist in, say, 1950, without using special tools to extend their mind. But part of me wonders if a more radical expansion of what a theory is may be needed..
Victor points out that we have, of course, built tools enabling us to see wavelengths of light we cannot see, to hear sounds we cannot hear, and so on. And perhaps, as the title of his talk suggests, it is possible that we can build tools to enable us to think unthinkable thoughts.
These are remarkable ideas. Of course, they are not without precedent. Many people have developed related ideas, including William Ross Ashby, Douglas Engelbart, and Seymour Papert, to name but a few. But, in my opinion, Victor's development is unusually promising and deep. I'm writing these notes to help me understand what Victor is doing, how he's doing it, and some promising directions for further work. I also intend to relate Kill Math to my own creative work, and hope it will help inspire some new directions.
The notes were more difficult to write than I expected. In retrospect, I can see that while Kill Math is easy to read, it is very challenging to understand at the deeper level that would enable one to do similar work. (I make this mistake with nearly every work I wish to understand well. Mea culpa. ) Part of the reason is that I have much less design and programming experience than Victor** And, I would guess, a different kind of experience with mathematical research, which creates another barrier to understanding., and the deeper I got, the more keenly I felt this deficit. More on this later.
Through the remainder of these notes I will use the convention that unmarked quotations are from Kill Math. Quotes from other sources will be explicitly marked.
Two examples: interactive difference equations and scrubbable numbers
Historian Charles Weiner, interviewing physicist Richard Feynman, discussing Feynman's physics notebooks: These are loose-leaf notebooks with each page containing your work, everything that you asked yourself... And so this represents the record of the day-to-day work.
Feynman: I actually did the work on the paper.
[...]
Weiner: Well, the work was done in your head but the record of it is still here. Feynman: No, it's not a record, not really, it's working. You have to work on paper and this is the paper. Ok?
To make the ideas in the previous section more concrete, let
me show two prototypes that Victor has created. The first is
a video demonstrating a medium for understanding difference
equations. The video is best watched fullscreened, which can
be done by clicking the four-arrow icon
in the bottom right of the video player:
As I wrote in my essay
Reinventing
Explanation, this medium "enables many powerful
operations, such as: tying parameters together; the
instantaneous feedback between symbolic and graphical views of
difference equations; and the language for searching over
functions. [Bret Victor has] created a vocabulary of
operations which can be used to understand and manipulate and,
most crucially of
all, play** There is a
beautiful
talk by Steven
Wittens where he demonstrates vividly how powerful play
can be in mathematics. Related ideas are explored in Seymour
Papert's Mindstorms.
My experience when learning a new area of mathematics is that
there is often a long period of time in which working with it
is quite painful. The simplest things are very difficult to
do. But after many hours you pass some sort of threshold.
Things begin to speed up, and it becomes very enjoyable to
work with the objects in your new domain; you become able to
play. At that point, the rate at which you are learning
speeds up dramatically. Well-designed media for thought may
speed up this process of getting-to-play. with
difference equations. And with enough exposure to this
medium, we'd begin internalizing these operations: we'd begin
to think about difference equations in this way."
The difference equation medium is very interesting. But it's easier to analyse a simpler and cruder precursor, namely, Victor's Scrubbing Calculator.
Let me show the scrubbing calculator in action, solving a problem that would ordinarily be solved with (what we think of as) algebra. You can see the details of the problem and its context in the essay linked in the last paragraph. The basic gist is that Victor asks us to consider a (real) design problem that came up when he was designing the graphics for a book. The design problem was to figure out how large to make the height of the horizontal bars in a bar chart, in order that the chart fill up the available space. The size (768 px) of the available space as well as the margins (60px and 140px) and the gaps between bars (20px) were already known, but could be slightly adjusted if necessary. This problem would, of course, conventionally be solved using algebra. Click on the play button below to see a different approach:

What's going on is perhaps already obvious from the earlier video, but just to spell it out: he's typing in his existing constraints on the margins and gap, and making a guess for the bar height. Then he scrubs over the value for the bar height until the answer on the right is what he wants, with some minor adjustments to other quantities.
Here's another example, which illustrates some different ideas. In this case, Victor is using the scrubbing calculator to split the bill for a road trip. His friend Andy paid 2910 dollars during the trip, while he (Bret Victor) paid 426 dollars. How much money does he owe his friend, in order that the bill be split evenly? To solve the problem, Victor "connects" two quantities in the equations, so they are tied together:

Think about how you'd solve this problem ordinarily. You'd set up a system of two linear equations, take the difference between the two equations, move terms from one side to the other, and so on. In other words, you'd go through a series of complicated formal steps which seem almost completely unrelated to your goal (unless you happen to have a great deal of training). It's as though you're standing on one side of a park, looking over to the other side, and some teacher comes along and tells you that to get to the other side, you first need to walk in the opposite direction, up some back alley, then insert a quarter in a machine, be sure to stop and pet the dog, etcetera. Provided you follow this special incantation you are assured that you'll somehow end up where you wanted to go. It's black magic. In ordinary algebra, the operations performed do not obviously have very much to do with the goal. In the scrubbing calculator the operations you perform are directly related to the goal.
There is more to the scrubbing calculator (link): Victor also adds operations to "lock" and "unlock" numbers in the equations. I won't discuss those operations here, since we've already got quite a bit to be thinking about. But they're interesting, too.
What should we make of these examples?
As someone mathematically trained it's tempting to reflexively respond: "That seems harder than solving the relevant equations." That's true if you've already spent a great deal of time mastering traditional techniques for solving such equations. However, that's also an unfair comparison, and it's not clear whether someone learning this for the first time would have more trouble with algebra or with learning the scrubbing calculator. I suspect that many would find the scrubbing calculator easier, and some people would find it far easier. There's an old joke in which a mathematics professor begins posing a problem: "Suppose $x$ is equal to $15$...", only to be interrupted by a student: "But professor, what if $x$ is not equal to $15$?" My own experience in talking about mathematics with others is that there are many intelligent people with exactly this kind of block. And when someone is blocked in this way it's very difficult for them to really understand what's going on when manipulating algebraic expressions.
Another typical skeptical response to the scrubbing calculator
is to emphasize the value in learning to use the
abstract symbols. Of course, there is great value in learning
to use the abstract symbols, but it's a poor basis for
comparison. The value in the traditional approach is only
gradually revealed over years of mathematical training. We
should not expect to understand the value of the ideas used in
the scrubbing calculator all at once, in our first reflexive
response. We would need to develop the ideas in the scrubbing
calculator much further in order to understand the value in
this alternative approach** Much of
the online commentary directed at Kill Math
completely misses this point. You have people enumerating all
the great things about traditional analytic methods. Many of
those people have trained for years (or decades) with those
analytic techniques, yet have only a few minutes exposure to
the alternative techniques. For many examples of this style
of commentary, see the
comments here.
Of course, detailed criticisms in this vein may be stimulating
as a way of
improving the medium (see,
e.g., Evan
Miller's essay), but they have little value as a means of
evaluating the potential of the medium. I must admit I find
it strange that there are people out there who believe they
must stridently defend a system of thought that gave us
electricity, the moon landings and the automobile, from (what
they perceive as) a determined attack by one guy armed with an
iPad. Sheesh.
Incidentally, this erroneous approach to evaluating the
potential of anything new is so common, across so many fields,
that I wonder if it shouldn't be regarded as a cognitive bias,
along the lines of things like confirmation bias and the
fundamental attribution error. This "foresight bias" seems to
be correlated, in my experience,
with hindsight
bias: looking at the past and seeing how it all obviously
came out just so. . In essence, we're comparing a few
minutes exposure to a medium developed by one person with
thousands of hours of training in a tradition that has been
developed over thousands of years by thousands of people.
It's perhaps not so surprising that the latter has some
advantages! But focusing myopically on those advantages
doesn't help us see what new and different potential there may
be in the scrubbing calculator. It's like trying to
understand cubism's potential to transform how we see by
looking only at Braque's first cubist paintings:

Good luck with that!
What makes the scrubbing calculator seem remarkable to me is that it develops new atomic operations which we can use to think about mathematics. I've shown two such operations: the basic scrubbing operation, and the "connection" operation. We also saw several such operations with the difference equation medium, e.g., the act of searching over an expression. More subtly, the notion of instantaneously graphing an expression is, I believe, a new basic operation; it changes the experience of mathematics.
In the case of the scrubbing calculator these atomic operations are introduced as a means to a particular end, namely, allowing people to solve algebraic problems while working with concrete numbers:
This work is about allowing people to solve algebraic problems while working entirely with concrete numbers, instead of abstract symbols. We are accustomed to assuming that variables must be symbols. But this isn't true — a variable is simply a number that varies. If we are able to vary numbers interactively, then we don't necessarily need to name them... We conventionally use rote algebraic mechanisms to convert the equation into an explicit expression. But this is not paper, and a computer has no trouble calcuating an implicitly-defined number... [We also] use $x$ to mean, "There is a single number that should appear in two different places"... But this is not paper, and a computer has no trouble keeping track of multiple instances of an object. With a calculator like this one, we can connect numbers to make them the same, instead of having to name them.
This passage emphasizes the computer's ability to enable new atomic operations. It strikes me that although these atomic operations were introduced in response to a specific problem, they can potentially be repurposed and used to serve other ends. In other words, we can take these new atomic operations and try them out in new contexts, trying to push them as far as they can go. The most powerful will, no doubt, turn out to be extremely useful in a wide variety of contexts** There's a related phenomenon in mathematics: surprisingly often, famous results began life as lemmas in papers whose "main" result is now forgotten. Instead, it was the lemma, originally just a waystation along the way to proving some "important" theorem, which was found to be of utility in many other contexts. You might ask: why not just aim at the lemma? I'm not sure it can be done. The utility of such lemmas is usually that they can help solve a wide variety of hard problems. And so it is natural that they are first discovered en route to solving a specific hard problem. Absent such problems, I don't know that it's easy to determine which tools will be most powerful. .
Everyone who learns mathematics understands that how we think is strongly influenced by the elementary operations and representations available to us. Think of how decimal notation enables us to reason in much more powerful ways than roman numerals. Or about how the invention of co-ordinates made possible a new approach to geometry. Much of the history of mathematics has been about expansions in our reasoning power enabled by the invention of new mathematical objects, and by the invention of new ways of representing and operating on mathematical objects.
Historically, those representations and operations have been constrained by the accident that we're using paper and pencil as our medium. Changing the medium enables an expansion of those representations and operations:
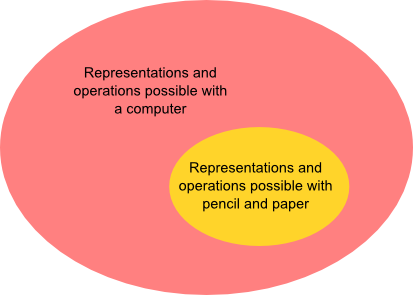
Representations like the scrubbable numbers and operations like connecting two numbers are examples of this expansion. But, of course, there's no more reason for them to be an endpoint than there was for Roman numerals to be the endpoint of what we did with paper and pencil** The Romans, I believe, actually used papyrus and a primitive form of pen. But those media seem to have offered very similar expressive capabilities to today's paper and pencil. .
One problem with the diagram above is that it conveys a monolithic impression of what a computer is. Namely, a computer is either: (a) a thing with a qwerty keyboard, a mouse, a flat LCD monitor about 20-30 inches in linear dimension; or (b) a flat device, about 4-10 inches in linear dimension, with a touchscreen which you manipulate by tapping and swiping. Of course, it's a historical accident that these are the dominant modes of interaction right now, and it will certainly not remain true in the future. It's interesting to ask questions like: what new representations and operations become possible when you're using a kinect? A wii remote? A leapmotion device? An Oculus? You can ask questions like: how would you interact with your voice? With your eyes (using eye-tracking and similar tools)? With motions of your body? I suspect that even taking a silly question seriously – say, what kinds of interaction can you do with your elbow – may be enlightening. And, of course, you can turn it around, and ask questions like: what hardware and interface would let us best explain (or explore) general relativity? Or molecular biology? Or quantum mechanics** Had this question been seriously asked in 1970 I suspect quantum computers would have been invented earlier. Feynman's pioneering 1982 paper on quantum computing started from a related question, namely: what kind of computer would you need to use to simulate physics??
A second problem with the diagram above is that the representations and operations currently possible with a computer are not, strictly speaking, a superset of the representations possible with paper and pencil (and related media, such as whiteboards). There are important ways in which the latter media remain superior. What would we need to make computers entirely superior to paper and pencil? To a whiteboard or blackboard?
Scrubbable numbers over many levels of granularity
At the end of Victor's essay on the scrubbing calculator, he poses the following exercise:
Granularity. Some numbers need to be adjusted over large ranges — you may want to go thousands in one stroke. Other numbers might need multiple decimal-point precision. The tool can't necessarily infer which is which. Can you think of a UI that could accomodate adjustments at different levels of granularity?
In this section I describe the outcome of my first set of attempts at this exercise. I'm not a designer and have very limited experience writing programs that run in the browser, so my progress has been limited. The main value for me has, rather, been in gaining more understanding for what's involved in the design process, in particular the rich set of questions thrown up in tackling what seems like (but turned out not to be) a mundane problem, and the value of iterative analysis.
Here's a first, very rough sketch. In the equation below, mouseover either number on the left of the equation, click on one of the revealed icons, and hold down the mouse button while adjusting the number.
This gives us more flexibility than the original scrubbable numbers, because we have the ability to adjust numbers both linearly and exponentially. However, it has a number of deficiencies.
Some of the deficiencies are relatively minor problems with the look and feel, including: (1) The expansion and contraction of the scrubbable numbers causes distracting changes to the overall layout of the equation, which need to be fixed. It would also perhaps work better if the icons were below rather than alongside the numbers; (2) The icons need to be more responsive, perhaps changing in more obvious way to indicate they've been selected, and the colour choices could do with more work; (3) There are some inconsistencies in the way highlighting is done that should be ironed out. It's easy to make progress on these and many other problems with just a little more work.
However, one really serious deficiency is that this approach severely limits the class of numbers you can reach. To see the issue, suppose you use the exponential slider to increase a number out to near (say) 1 billion. Then each increment of the slider moves you by an amount of about 100 million. You can use neither the exponential nor the linear slider to adjust over that entire range. And so many numbers are essentially inaccessible.
I'm somewhat embarassed to say that I didn't anticipate this difficulty in advance. In a backhanded way, that's encouraging: this new representation made a problem obvious which I didn't see initially, despite having spent hundreds of hours of my life thinking about exponential versus linear growth!
Can we do better? In the equation below, click and hold on one of the numbers on the left-hand side, and then slowly drag the mouse quite a ways to the right (or left), while continuing to hold down the button. Then repeat the process a few times, to get a feel for what's going on. Note that for this particular problem, we don't actually need to explore over many orders of magnitude, and so this approach is overkill. Still, it's a context that's familiar from Victor's example above.
A little experimentation will show that scrubbing here has a nonlinear response. When you're near the number, it changes by a small amount. As you get further away, it starts to change by larger and larger amounts. This allows both very small and very large (albeit coarse) adjustments. The advantage, though, is that by making a few adjustments we can reach an arbitrary number. In essence, we begin our exploration by finding the right order of magnitude, and the most significant digit, then explore to find the second most significant digit, and so on.
Of course, there are still many deficiencies. The design could do more to unobtrusively cue the user as to the expected behaviour. We have limited range of motion on the left, which makes decreasing numbers somewhat awkward. I explored several response functions, and the one implemented is the one that worked the best on my machine, with its particular mouse behaviour and screen resolution. However, I wouldn't be surprised if a thorough systematic investigation resulted in a better response function.
A serious problem with the above demonstration is that the context is wrong – we simply don't need to vary the margins and so on over many orders of magnitude. It'd be better to look at a problem which provides a more informative context.
Consider the following problem about world population. Let's assume that world population growth is 1 percent per year, and we're interested in knowing: what does the population need to be today, in order that in 20 years time the population will pass 10 billion? This problem is, of course, somewhat artifical, but we'll still learn some useful things by considering it. Try repeatedly scrubbing over the first number in the following equation:
Some experimentation suggests that it might make sense to give the slider some memory. In particular, the natural way to explore is first to get the overall order of magnitude about right, then to explore one or two orders of magnitude lower, then one or two orders of magnitude lower, and so on.
Another idea is to give the slider some notion of momentum and damping. In particular, if you move the mouse quickly that usually means you want to increase the rate at which the number is changing, while if you move the mouse slowly that usually means that you want to decrease the rate at which the number is changing. I expect considerable experimentation would be necessary to get this to work well, but it might be worth the effort. Note that there has been much prior work on similar notions in user interfaces, and it may be worth looking at that work.
Another natural idea to explore is allowing the growth rate (or number of years) to be scrubbable. This gives rise to an interesting problem. Arguably, the natural way to scrub the growth rate involves only a linear response. If we take this point of view, then we'd need to figure out some way of cueing the user to the difference between srubbable numbers with a linear versus a nonlinear response.
The problem with this point of view is that we don't know in advance what type of response is needed. In an ideal world, we would have a single, unified interface. Unfortunately, when I tried using the nonlinear response with the growth rate it felt unnatural: it changed too quickly. I also tried slowing things down, by making changes linear over two orders of magnitude (instead of just one). That felt unnatural in a different way. It's possible, however, that with further experience one or both these options might come to seem more natural, and to be acceptable. Or perhaps more ideas are needed.
Another problem with our current scrubbable numbers is that there is (currently) a minimal scale: the minimal increment or decrement in the examples above is $1$. You could easily change this, to be, say, $0.1$ or $0.01$, but there would still be a minimal scale. And for some problems we don't know in advance what the minimal scale should be. Can we find some way to be able to both increase and decrease the scale of the scrubbing?
I won't try to address all these questions here. Still, it's obviously fertile ground for exploration, and might be fun to come back to.
Comparison to Mathematica and other existing systems
How do the ideas in Kill Math relate to systems such as Mathematica, Maple, Matlab, and so on?
A skeptic may, for instance, respond to Kill Math with: doesn't Mathematica (or some other such system) already offer a new interface to mathematics? Isn't Mathematica tremendously useful? Shouldn't we focus our efforts on this kind of system, or open source alternatives such as Sage?
Let me begin by pointing out the obvious, so I don't lose sight of it: of course the ideas in Kill Math are radically different than in the other systems. This is immediately evident upon simply looking at the prototypes. The problem is to understand and articulate what the differences are, and what is new in Kill Math.
For concreteness I will begin my analysis by comparing Kill Math to just one system, Mathematica. Then I'll turn to other systems.
Mathematica is certainly tremendously useful. But that doesn't mean it's doing the same thing as the prototypes in Kill Math. Consider the type of problems typically solved by Mathematica. Amongst the most common are:
- Integrating an expression.
- Solving a set of equations.
- Simplifying an expression.
- Substituting a value into an expression.
This looks like 19th century mathematics. However, what is new here is that: (a) the solution to the problems is automated, and can be done with no (or little) human intervention; and (b) the scale at which these activities can be carried out – it is not uncommon to use Mathematica to deal with expressions involving thousands of terms. Both these abilities qualitatively change how people engage with mathematics, dramatically enlarging both the class of problems they're willing to attack, and the class of problems they're able to solve.
However, note that each problem in my list above is of a type that would have been familiar to 19th century mathematicians, the data specifying the problem is given in a form that would have been familiar to 19th century mathematicians, and the solution to the problem is given in a form that would have been familiar to 19th century mathematicians.
In these senses, Mathematica doesn't change what we think mathematics is. Many of the core objects and operations would have been familiar to a 19th century mathematician.
Are there any ways in which Mathematica does change what we think mathematics is? Well, Mathematica does introduce several new fundamental objects and operations into mathematics, when compared to 19th century mathematics. In particular, graphs, animations, and notebooks are all new fundamental objects, with associated fundamental operations. Of course, things like graphs and notebooks (less so animations) have long been part of mathematics. But the benefit in Mathematica is that we can operate on them, that is, we can perform programmatic operations involving graphs, animations, and notebooks. Put another way, we can treat these as things in a way impossible with paper and pencil. On paper, a graph is a tremendously complex aggregate typically involving hundreds of strokes of the pen. It's difficult and time-consuming to manipulate. On a computer it may be treated as a single object which can be manipulated in powerful ways using single commands.
Ideally, these new objects will be data structures with a beautiful, clean, and powerful interface, one that integrates well with the rest of Mathematica, and makes it possible to programmatically reason about these objects. For instance, with a well-designed interface it ought to be trivial to say things like: plot this graph over many random choices of such-and-such parameters, and find the version of the graph which shows the greatest divergence in behaviour between these two quantities of interest. Or to say: contrast the complexity of underlying reasoning used in two different notebooks (say, two different proofs of the same theorem). Or to say: pipe the output from these two notebooks into this other notebook. And so on. Broadly speaking, as designers of such a system we want to ask questions like: What new classes of object can we introduce? What are powerful operations that could be performed on these objects? And: Are there powerful new data structures we can build from these objects (and associated operations on those data structures)? By doing this we make it possible to think in powerful ways about these new objects. We are, in a real way, enlarging the space of thoughts we can think** Incidentally, there is another class of new objects added in Mathematica, beyond notebooks, graphs, and animations. That's very large expressions. 100 years ago it was not practical for a mathematician to deal with an expression involving 10,000 terms, unless there was some regularity that enabled them to deal with many terms at once. Certainly, one couldn't treat such an expression as a single object which can be manipulated in powerful ways. Nowadays, it is routine to deal with such expressions, and there are powerful operations which can be performed with such expressions; there is a real sense in which we can now think about such expressions, when formerly we could not. This is another example of enlarging the space of thoughts we can think..
Now, I'm not a Mathematica guru, but my impression is that the ideal described in the last paragraph isn't quite what's happened. Many of these things are in principle possible in Mathematica. But that doesn't mean they are always easy and natural. For example, you'd like for it to be trivially easy to inspect, manipulate and reason about the contents of Mathematica notebooks, having powerful tools to access things like the parse trees and the chains of transformation rules used by Mathematica to solve problems. That may well be possible – I don't know enough about Mathematica to be sure. But my experience with Mathematica suggests that it's certainly not what the system was designed to do. With that said, the system has gradually evolved in this direction, with these new objects and operations gradually becoming more powerful, and moving toward becoming first class mathematical citizens. However, it does not appear to have been a high priority to push the design of those new objects and operations, nor to make them central to the system.
Mathematica looks to me like what you get when a very competent and creative traditionally trained mathematician** Wolfram's PhD was, in fact, in theoretical physics. For my current purposes, though, the difference doesn't much matter. (Indeed, there's a lot of overlap between the two in training). designs a system for doing mathematics. The problems it solved, at least in early versions, are exactly the type of problems that competent and creative mathematicians have been interested in for decades or centuries. And so the mathematics started out represented in very conventional ways. The system has only gradually added new fundamental classes of object and operation.
By contrast, the prototypes in Kill Math look to me like what you get when a very competent and creative designer starts designing systems for doing mathematics. What's at issue is what fundamental objects, operations and representations we should be using. Think about some of the operations introduced in the prototypes above:
- The operation of "tying" two quantities together, to form a single linked entity.
- The operation of scrubbing a number.
- The operation of "searching" over the graph.
- ...
These operations are, in turn, associated to new fundamental objects, such as tied numbers, and search expressions for the graph, as well as redefining the way we think about old objects: a scrubbable number is not the same as an ordinary number, in important ways. In particular, scrubbing enables new kinds of exploration and play. That may sound like an exaggeration, and perhaps it is when we're dealing with very simple prototypes, but as the prototypes become more sophisticated it makes more and more sense to think of scrubbable numbers as truly a different type of object. Imagine you are playing a first-person shooter game, but instead of directly controlling the motion, you instead repeatedly have to type in an angle describing the direction you're facing. This would change your relationship to the game, and not just in the obvious sense that it would slow down the rate at which you could control the game; it would change the sense of control, and give you much less visceral feedback. Scrubbable numbers point the way toward a different relationship with numbers.
This all sounds very wishy-washy and touchy-feely: the "relationship" we have with numbers? Yet I think it's at the heart of what it means to understand something. Littlewood is supposed** The story is amusing. Littlewood was reading the proofs of some remarks by Hardy on Ramanujan: "as someone said, each of the positive integers [etc]". Littlewood responded: "I wondered who said that; I wish I had". In the final version it read "It was Littlewood who said...". Littlewood: "What had happened was that Hardy had received the remark in silence and with a poker face, and I wrote it off as a dud. I later taxed Hardy with this habit; on which he replied: `Well, what is one to do, is one always to be saying "damned good"?' To which the answer is `yes'.". The story is from Littlewood's beautiful Miscellany. to have said of Ramanujan that "each of the positive integers was one of his personal friends". That's a statement about the relationship Ramanujan had with the integers. It's the quality of that relationship which was, in part, why Ramanujan was such a great mathematician.
Returning to Kill Math, and to sum up, an important way it differs from Mathematica is in focussing on identifying new types of mathematical object, new representations (both for new and old objects), and new operations (again, both for new and old objects). All this happens to some extent in Mathematica, but it is not the design goal in the same way as in Kill Math. Rather, I believe Mathematica's core focus is on outsourcing cognition: doing the kind of cognitive tasks mathematicians have always done, but much faster, and more reliably. The expansion of what mathematics is is a more incidental goal. Both goals are, of course, worthwhile; Mathematica (and systems like it) are, for the time being, much more mature. It is interesting to imagine some future system which takes both goals very seriously.
A parenthetical remark on notebooks: Notebooks are interesting as a new way to represent and experience a collection of mathematical ideas. A nice example to convey the flavour comes from this iPython notebook by Peter Norvig. It's in Python, but similar things can be done with Mathematica notebooks. The link takes you to a static web version of the notebook, but the important thing is that you can download the notebook and execute it. When you do that, what the notebook offers is an experience of certain important mathematical ideas. Another person can go in and begin to tweak and extend and even transform the ideas Norvig is expressing. The notebook provides a vivid demonstration of counter-intuitive results, which can provoke questions, and provide a relatively easy way for a person to then answer those questions. In other words, it's creating a genuine experience of non-trivial mathematical ideas; an experience of being able to play with them, in the terminology I used earlier. That's something that only a tiny fraction of the population have ever experienced. Now, a similar experience could have been created with 19th century tools. But it would have been pretty darn difficult to achieve, and hard to scale the experience. With Mathematica or a tool like ipython it becomes much easier. Note, however, that while playing with short Python scripts is easier than conventional mathematical modelling, it's still a relatively inaccessible intellectual activity.
What about systems other than Mathematica? I have only a little experience with systems such as Matlab, Maple, and Sage. My impression is that many of my remarks about Mathematica apply to those as well. In particular, many of the core objects and operations in those systems are objects and operations well understood by 19th century mathematicians. New objects and operations have been added, but it's mostly been done piecemeal, in a rather gradual fashion, in a manner similar to that I described for Mathematica. Again, it does not appear to have been a high priority to push the design of those new objects and operations, nor to make them central to the system.
There are, of course, many systems for exploring mathematics that I haven't listed above. Think of Coq, Wolfram Alpha, D3, R, Julia, Prolog, Logo, Scratch, Haskell, and others. All of these are, in their own ways, different to both Kill Math and Mathematica** Wolfram Alpha is an extension of Mathematica, but is fundamentally different in enough ways that it requires a separate analysis. The same seems likely to be true of Wolfram's new programming language, which I have not yet looked at in any detail., and require their own analyses. I am not yet sufficiently familiar with these systems that I'll attempt a detailed commentary. I will, however, note that these systems also add new first-class objects and operations. In particular, they reify data sets and proofs: these become things that can be inspected, manipulated, and related to other objects. However, I do not know to what extent this sort of extension is the raison d'être of these systems, and to what extent it's simply an unintended consequence of other design decisions.
Moving theorems into the user interface
Theorems express surprising connections between mathematical concepts. Think of the way the fundamental theorem of arithmetic connects the positive integers to the primes. Or the way the Cauchy-Schwarz inequality connects inner products and lengths. The information the Sylow theorems give us about the size of subgroups of a finite group. The fundamental theorem of algebra tells us that there is a root for every non-trivial polynomial over the complex numbers (or, equivalently, that such a polynomial can be factored into monomials). And so on. Ideally, such connections should be made visible through the user interface. That is we should move theorems into the user interface. Tipping it upside down, we can view theorems as challenges to develop a user interface which reifies those theorems in a powerful way, providing the user with cues that help them reason, and representing mathematical objects in ways that help suggest the relevant operations and relationships.
Knuth once said:
I have been impressed by numerous instances of mathematical theories that are really about particular algorithms; these theories are typically formulated in mathematical terms that are much more cumbersome and less natural than the equivalent formulation today's computer scientists would use.
We can go much further. Theorems are traditionally presented as static statements about the relationship between mathematical objects. But the static nature of theorems-of-statements is a consequence of historical accidents about the media we've used to represent mathematics, not of the fundamental nature of mathematics. We could equally well have theorems which are actively reified in the environments in which we think; they respond to what we do, they cue us when needed. That is, they're visible, active parts of the mathematical process. The theorems start to become part of the mathematical objects themselves. This point of view seems to me to be much more natural.
Let me give an example that moves a tiny, tiny bit in this direction. It's not what we'd usually call a theorem** I'm really using the word "theorem" as shorthand for "non-trivial mathematical connection"., but it's a very simple example of the sort of connection often made in theorems. It illustrates how the value of $\sin(\theta)$ is just the $y$ co-ordinate for a point on a unit circle at an angle $\theta$ from the horizontal axis. Try clicking and dragging to adjust the angle on either side of the frame. Or click "Start" to see how the behaviour changes as $\theta$ changes** This design is not mine, nor do I know where the idea originated (I have seen variations on this idea many times, in slightly different forms)..
This provides a vivid, concrete demonstration of a connection that many students miss, even after spending tens or hundreds of hours "learning trigonometry".
While the demonstration is nice, one shortcoming is that it's primarily about explanation, not discovery. Explanation is valuable, but it's also a much less challenging context than discovery. When you're doing discovery you don't know what results to apply.
To unpack that a bit further, let me discuss another example: Euclid: The Game. In level 1 of the game, the player is presented with two points, A and B, shown below:
The player is asked to use five tools – the five icons on the top left – to construct an equilateral triangle. The tools do things like inserting a line segment, or constructing a circle with a specified center and specified edge point (which could be, for example, points A and B). By using those tools in just the right way, we can construct an equilateral triangle as follows:** The annotations – "Smart!", "Well done!" etc – are not mine. They're encouragement the game gives you along the way, if you're making the right moves.
So we now know something new: we've learnt how to use the elementary tools to construct an equilateral triangle. Here's the next level of the game:
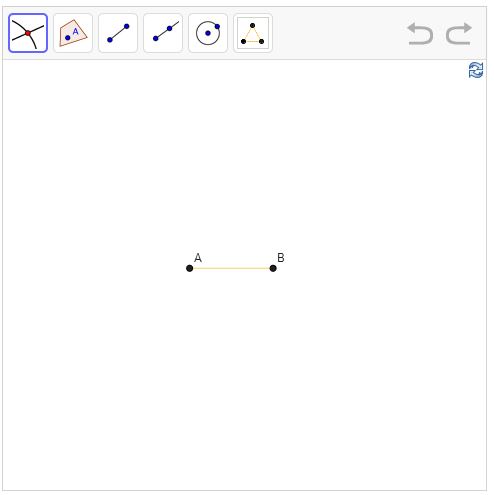
If you look closely, you'll see that there is a new icon in the top row, representing our ability to construct an equilateral triangle. We're growing a user interface, moving the mathematical relationships we discover into that interface. And as a result we can see what we know about different mathematical objects.
Many of the ideas in the game could be taken further. While playing I often didn't understand my own puzzle solutions very well. I'd play around for a while, develop some understanding, but also (often) get a little bit lucky. The result was that I'd add an extra tool into my geometric kit, without always understanding in depth why what I'd done worked. It might aid understanding if the game recorded constructions, so that we can replay and edit those constructions, and, perhaps, do other sorts of analysis. For instance, it might be possible to turn the game into Euclid Golf: challenge people to find constructions that are the simplest possible (e.g., required least effort, in some natural metric). So you'd be told "You solved this puzzle with 5 operations, but it can be done in 4". The requirement of minimizing the constructions will tend to increase understanding, as people take their initial, imperfect solutions, and try to understand what is essential, and what is cruft that can be eliminated. I'm not sure this would work: many of the "random" solutions that people are producing are already minimal or near-minimal. But there is, at least, the seed of an idea here, which might make a nice future project.
Another problem is that we know so much. Think of all the different geometric constructions that we know. How could we fit all those thousands of constructions in a natural way into a user interface? Without some clever ideas the interface is going to be too confusing to be useful.
This problem arises also in other contexts. Imagine now that we're working on some mathematical problem, and we write down $n$ to denote a positive integer. In an ideal mathematical super-notebook, we'd potentially see $n$ in many different ways. For instance, perhaps the most famous representation is that every positive integer is a unique product of primes** Note, by the way, that I'm not saying that when you write down an integer — say, 91 — the system you're using should immediately show you its prime factorization, 7 x 13 (although this might also be useful). I'm saying that it should be possible to tell your system "Consider a positive integer, $n$,...", without specifying its value. The system might then remind you that $n$ has a unique prime factorization $p_1^{m_1} p_2^{m_2} \ldots p_k^{m_k}$, and help you reason with this and other alternate representations.. But that's just one of thousands of representations known for positive integers. How do we know which representations are relevant in any given context?
The art of mathematics is very often in choosing which representation to apply in order to obtain insight. A good mathematician internalizes many different representations, understands how they relate to one another, and in what contexts they tend to be applied. A good user interface would reflect this plethora of possibilities, and help hint or cue you to use the right representation at the right time. This is what I was referring to above when I said that explanation is a much less challenging context than discovery. When you're doing the kind of exploration that leads to discovery you don't necessarily know what results to apply. Thus, it seems to me to be a much easier problem to design user interfaces for explanation than for discovery.
I've made a few initial on-paper attempts at user interfaces for discovery. I learnt a lot while doing this work, but the resulting designs were rather unsatisfactory. I may recount some experiments along these lines in future notes – it's worth thinking about what went wrong. Certainly, this is a problem deserving sustained effort! I will make three comments that occurred to me while working, however.
First, on the richness of the user interface needed to do discovery: there may be a considerable advantage to using a 3d environment, like that provided by the Oculus Rift. Having 3 spatial dimensions will enable interfaces that let users work in a far richer and more complex choice environment than is currently the case; enough to make a dramatic qualitative change in the experience.
Second, I found it helpful to begin my experiments by picking a piece of simple but genuine mathematics where it's possible to give a plausible account of discovery. Having an existing narrative of discovery helped in stimulating user interface ideas. My initial experiments were with the main result from a paper I wrote in 1999. It solves a simple but fundamental problem about the representation of states in quantum mechanics. The benefits of this were: (a) I have a pretty good idea of how the result was discovered** This sounds facetious, but is not. I don't think we really know what's going on in our own heads when we make a discovery. It would not surprise me if the most important factors are largely unconscious.; (b) the argument is extremely simple; (c) it's an argument based largely on switches of representation. In particular, I made use of a representation theorem that was not common knowledge in the quantum physics community at the time.
Third, it seems to me that an environment for doing mathematics needs an exquisite, supremely flexible and expressive type system.
Let me see if I can explain what I mean by this. First, what I'm not saying: I'm not talking about what theorists of programming languages call the theory of types.
To what I am saying: suppose I'm investigating a problem in quantum computing, and in the course of the problem I encounter some matrix, $M$, which I realize is central to the problem. As soon as I see such a matrix, all sorts of connections are made – I will have in mind results like: (a) the singular value decomposition; (b) the Schur decomposition; (c) the fact that the matrix has at least one eigenvector (if it's a complex matrix), and so on. I may suspect that the matrix is Hermitian. Often that can be proved with just a little extra work. If I can do that, then I immediately add a few extra facts: (d) the matrix is diagonalizable by a unitary matrix; (e) the matrix has real eigenvalues on the diagonal; (f) the singular values are the absolute values of the eigenvalues, and so on. Having established the Hermitian property, I may suspect that the matrix is positive. If I can establish that, I get access to another new slew of facts. And so on. Ultimately, one ends up reasoning about objects where you have long lists of properties: this is a positive, Hermitian matrix, with such-and-such a gap between the first and second largest eigenvalues, the trace is such-and-such, etcetera. You must be able to hold all those properties in your head, understand the implications of the properties, and how they relate to one another.
What I am trying to convey here is that when reasoning about mathematical objects we constantly learn new things about those objects, and that changes our internal representation of the object. That is much of what doing mathematics is: little incremental increases in knowledge, noticing this and that property, gradually building up our understanding. This process of constantly updating one's understanding is not like the type system used in most programming languages, yet it seems close in general spirit. What we want is a type system which is flexible enough to express all these many, many properties. When thinking about problems the kind of thing I find myself thinking is "Well, this matrix has a pretty large spectral gap, but not too large, it's about a factor such-and-such smaller than for this matrix over here, and it seems like it might be related to the gap in such-and-such a model". What sort of type system would support such a statement?** Ideally, the type system would allow some ambiguity, which is often extremely helpful when getting a feeling for a mathematical problem. But even an expressive system without much tolerance for ambiguity would be useful.
When I look at existing systems for doing mathematics, I don't see this. For instance, when I'm using Python / Numpy to do linear algebra I have very limited ways of expressing even such basic facts as that a matrix is Hermitian, or unitary, much less the actual way in which I think about the objects, in terms of great collections of interrelating properties. And because the system is so unaware of the actual nature of the mathematical objects it's manipulating, it has no means of helping express what I know (or ought to know) about those objects. It's not visible even at the level of long textual lists of possibilities, much less in well designed and suggestive visual representations.
I've used the term type system here with some trepidation. The term doesn't have quite the right connotations: people think of type systems as dry things, not as things connected to beautiful, expressive user interfaces. But I'm thinking of the type as being intimately connected to the user interface. In this view, a scrubbable number is not the same type as an ordinary number. In other words, when I say "type" I'm really referring both to a rich concept of what a mathematical object is, and rich ways of allowing the user to interact with it, and to relate it to other objects** I suspect programming languages such as Haskell achieve some (but not all) of what I've described here; they have far more expressive type systems than more traditional programming languages, but also fall far short of the rich ways we think about mathematical objects. I do not (yet) know enough about this vein of work to be sure, though. Notions such as duck typing and extreme late binding are also relevant; one learns about mathematical objects in real time, and the representations and interface change in response. Also relevant are Coq and the Curry-Howard isomorphism, which I currently know little about..
Let me finish this section by zooming out a little to the long view. Consider the following story from Thurston, about how we think about mathematics:
How big a gap is there between how you think about mathematics and what you say to others? Do you say what you're thinking?... mathematicians often have unspoken thought processes guiding their work which may be difficult to explain, or they feel too inhibited to try... Once I mentioned this phenomenon to Andy Gleason; he immediately responded that when he taught algebra courses, if he was discussing cyclic subgroups of a group, he had a mental image of group elements breaking into a formation organized into circular groups. He said that 'we' never would say anything like that to the students. His words made a vivid picture in my head, because it fit with how I thought about groups. I was reminded of my long struggle as a student, trying to attach meaning to 'group', rather than just a collection of symbols, words, definitions, theorems and proofs that I read in a texbook.
Why can't we create tools to convey that picture, and powerful means of working with it, as part of an environment in which to think and create?
Making the abstract concrete
To a certain extent, a person's mathematical skill is tied to their ability to [...] make the abstract more concrete.
Later in the essay, Victor quotes Oliver Steele in a similar vein:
Anything that remains abstract (in the sense of not concrete) is hard to think about... I think that mathematicians are those who succeed in figuring out how to think concretely about things that are abstract, so that they aren't abstract anymore. And I believe that mathematical thinking encompasses the skill of learning to think of an abstract thing concretely, often using multiple representations – this is part of how to think about more things as "things". So rather than avoiding abstraction, I think it's important to absorb it, and concretize the abstract... One way to concretize something abstract might be to show an instance of it alongside something that is already concrete.
I want to riff on these statements for a bit. The thoughts that follow are a bit more disconnected than previous sections, and so I've broken them up into three separate pieces, without attempting to impose an overarching narrative: (1) a discussion of examples of making the abstract concrete; (2) a discussion of so-called "genius"; and (3) a discussion of the utility of mastering new mathematical representations.
Examples: Let me give some examples where abstract concepts are explicitly made more concrete. A nice collection of examples comes from the answers to a question on MathOverflow** A non-trivial fraction of the discussion on MathOverflow is about making abstract concepts more concrete. This may be viewed as an empirical confirmation of the fact that mathematicians spend much of their time trying to understand mathematical objects in more familiar terms., asking how to think in more than three dimensions? It's instructive to look through all the answers, but I will quote just two here. The first is from Terry Tao:
[...] when dealing with the geometry of high-dimensional (or infinite-dimensional) vector spaces such as R^n, there are plenty of ways to conceptualise these spaces that do not require visualising more than three dimensions directly. For instance, one can view a high-dimensional vector space as a state space for a system with many degrees of freedom. A megapixel image, for instance, is a point in a million-dimensional vector space; by varying the image, one can explore the space, and various subsets of this space correspond to various classes of images. One can similarly interpret sound waves, a box of gases, an ecosystem, a voting population, a stream of digital data, trials of random variables, the results of a statistical survey, a probabilistic strategy in a two-player game, and many other concrete objects as states in a high-dimensional vector space, and various basic concepts such as convexity, distance, linearity, change of variables, orthogonality, or inner product can have very natural meanings in some of these models (though not in all). It can take a bit of both theory and practice to merge one's intuition for these things with one's spatial intuition for vectors and vector spaces, but it can be done eventually (much as after one has enough exposure to measure theory, one can start merging one's intuition regarding cardinality, mass, length, volume, probability, cost, charge, and any number of other "real-life" measures). For instance, the fact that most of the mass of a unit ball in high dimensions lurks near the boundary of the ball can be interpreted as a manifestation of the law of large numbers, using the interpretation of a high-dimensional vector space as the state space for a large number of trials of a random variable. More generally, many facts about low-dimensional projections or slices of high-dimensional objects can be viewed from a probabilistic, statistical, or signal processing perspective.
The second answer comes from Scott Aaronson:
Here are some of the crutches I've relied on. (Admittedly, my crutches are probably much more useful for theoretical computer science, combinatorics, and probability than they are for geometry, topology, or physics. On a related note, I personally have a much easier time thinking about $R^n$ than about, say, $R^4$ or $R^5$!)
- If you're trying to visualize some 4D phenomenon P, first think of a related 3D phenomenon P', and then imagine yourself as a 2D being who's trying to visualize P'. The advantage is that, unlike with the 4D vs. 3D case, you yourself can easily switch between the 3D and 2D perspectives, and can therefore get a sense of exactly what information is being lost when you drop a dimension. (You could call this the "Flatland trick," after the most famous literary work to rely on it.)
- As someone else mentioned, discretize! Instead of thinking about $R^n$, think about the Boolean hypercube $\{0,1\}^n$, which is finite and usually easier to get intuition about. (When working on problems, I often find myself drawing $\{0,1\}^4$ on a sheet of paper by drawing two copies of $\{0,1\}^3$ and then connecting the corresponding vertices.)
- Instead of thinking about a subset $S \subseteq R^n$, think about its characteristic function $f : R^n \rightarrow \{0, 1\}$. I don't know why that trivial perspective switch makes such a big difference, but it does... maybe because it shifts your attention to the process of computing $f$, and makes you forget about the hopeless task of visualizing $S$!
- One of the central facts about $R^n$ is that, while it has "room" for only $n$ orthogonal vectors, it has room for $\exp(n)$ almost-orthogonal vectors. Internalize that one fact, and so many other properties of $R^n$ (for example, that the $n$-sphere resembles a "ball with spikes sticking out," as someone mentioned before) will suddenly seem non-mysterious. In turn, one way to internalize the fact that $R^n$ has so many almost-orthogonal vectors is to internalize Shannon's theorem that there exist good error-correcting codes.
- To get a feel for some high-dimensional object, ask questions about the behavior of a process that takes place on that object. For example: if I drop a ball here, which local minimum will it settle into? How long does this random walk on $\{0,1\}^n$ take to mix?
Both these answers relate "how to think in high dimensions?" to problems that the authors of the answers already understand. Some of those problems, like thinking about a megapixel image, are problems that most people understand, even people with little mathematical training. In other cases, like thinking about characteristic functions, this is more specialized knowledge. However, the core in both cases is to represent the problem in terms of something you already have some understanding of. The deeper your understanding of the old representation, and the more powerful a connection you forge to the new problem, the deeper your understanding of the new problem. Note that the connection need not always be precise. As an undergraduate I worried a lot about how to think about high-dimensional objects. I was amused (and somewhat relieved) as a grad student to find that discussions of high-dimensional objects were often accompanied merely by a picture of a blob on a blackboard, yet the picture actually really did seem to help inform my intuition** Jen Dodd points out that this phenomenon may actually be quite deep: people need to go through a non-trivial process to learn how to do this kind of thing; and it's surprisingly helpful. The phenomenon may repay further investigation.! (There are, of course, various elaborations of this idea one can use – there's a nice example here.)
Neither of the answers above is quite about making the abstract concrete. Rather, they're about understanding the unfamiliar in terms of things we already understand well. Of course, when someone knows little about mathematics, that means explanations must be in terms of what we usually think of as the concrete. But when they learn more mathematics, they start to think of things like characteristic functions and the Boolean hypercube as concrete. It makes perfect sense to Scott Aaronson to talk about $R^n$ having exponentially many almost-orthogonal vectors. He's thought about this a lot; for him it's an important fact, a fact which is connected to many other things.
We've dwindled to the vacuously true. Everyone would no doubt agree that it's true that we should understand the unfamiliar in terms of things we already understand well. But so what? I think it's worth taking away a few simple observations: (1) Systems for doing mathematics typically assume that you've already gone through this process, and make little (or no) explicit effort to help with it; (2) Of course, such systems can be used as an aid to go through this process (e.g., I used Maple to learn about hypergeometric functions, by playing with plots). Doing this well requires some non-obvious meta-cognitive strategies; (3) These strategies could be reified within the system, either through user interface elements, or perhaps through less subtle methods, such as interactive essays which set up a playground for us to understand the new in terms of the old; and (4) It'd be interesting to relate this to the famous results in cognitive science on how the strength of our memory depends on the level of elaboration we bring to the act of memorization. E.g., the work by Craik and Tulving, and the followup work that's been done.
On genius: Most people have had the experience of talking with someone who seems to them to have lightning mathematical insight. You mention a problem to that person, something you have struggled with for hours or, in extreme cases, months or years. Voila, they solve it nearly instantly. What a genius!
This phenomenon occurs at every level, from elementary school to discussions amongst professional mathematicians. From the point of view of the person posing the problem, the "genius" appears to have special magical powers, abilities they do not have, and perhaps feel they will never have.
I believe this is wrong. I don't believe such a "genius" has access to some special ability that other people don't have. There is no such genius. What there is are people who systematically search out more ways of representing mathematical objects in terms of things they already understand well. They then slowly and laboriously practice using those many representations, until they come to seem simple and natural. This is more prosaic than the genius-with-special-powers story, but I believe it's more likely to be correct. More importantly, from the point of view of the current notes, it should be possible to support this process in the systems we build.
Mastering new representations can make it trivial to solve problems that otherwise seemed difficult or impossible. This is a reiteration of the last point, from a slightly different angle. I wanted to write down a concrete example of how mastery of new representations can trivialize formerly difficult problems. The example does not, alas, involve any nice new representations (a good followup problem). But I thought it might nonetheless be useful to keep in mind as an example of this process.
Suppose I ask you to prove that the square root of two is irrational, that is, it's impossible to write the square root of two as a ratio of two integers $m$ and $n$: \begin{eqnarray} \sqrt{2} = \frac{m}{n}. \end{eqnarray}
Now, let's suppose that you don't know a whole lot about number theory. Maybe you're a high-school student. But it just happens that you've really mastered the fundamental theorem of arithmetic, that is, the idea that every integer can be uniquely represented as a product of prime numbers. It's not just the case that you understand the statement and proof of the theorem, you've actively applied it in many different circumstances. If that's the case then it becomes second nature to try to apply it to problems involving integers, multiplication, and divisibility. You also tend to notice when it's possible to turn everything in the problem into an integer, which we can do by squaring the equation above, and moving $n$ to the left-hand side, \begin{eqnarray} 2 n^2 = m^2. \end{eqnarray} To someone used to thinking in terms of products of prime numbers it's obvious that the left-hand side has an odd number of prime factors, and the right-hand side has an even number of prime factors. This is impossible by the uniqueness of the prime factorization. And so our original assumption, that $\sqrt{2} = m / n$, must have been false, and we see that the square root of $2$ is irrational.
If you only know a little number theory, but just happen to have mastered the fundamental theorem of arithmetic, then proving the square root of $2$ is irrational is very nearly the kind of thing you can see in a flash of insight. But someone who happens not to have mastered the fundamental theorem (but otherwise has a comparable background) is likely to have a much tougher time seeing why the result is true. Certainly, the proofs I saw as a student were rather cumbersome, in part because they didn't assume that I'd really mastered the fundamental theorem of arithmetic.
Of course, it is perfectly possible for someone to have "understood" the fundamental theorem of arithmetic, yet still have trouble arriving at the proof above. The reason is that mastering the theorem doesn't just mean knowing the content. It also means: (a) knowing when it's likely to apply (problems concerning multiplication and division and lots of integer terms are often good candidates, problems involving lots of additions are often harder targets); (b) knowing when to apply heuristics like recasting your problem in a form where as many things are integers as possible; and (c) having considerable facility with basic algebra.
Problem: Develop a prototype environment which makes this kind of change in representation easier.
Questions / to do
I'll stop there with the notes. Obviously, this barely scratches the surface of what needs to be done, but at least I understand it better now. Let me conclude with a few final notes on things to explore.
Connections to other questions I am interested in:
- What comes after the web?
- If we were to start over, what would be the simplest system design that would support the most important of the basic capabilities of the web? (This looks superficially like the first question, but is in fact complementary.)
- Why is paper-and-pencil still so much better than a computer for so many types of exploration? What will change that? (Broadly: the really good pattern recognition that is now coming online, together with new hardware and UI design; this should open up entirely new worlds.).
- How to keep a notebook? This is a problem to which surprisingly little attention has been paid. Yet there's much to say about it, and it informs questions like "What's an ideal medium for doing creative scientific work?"
- Finally, let me mention a few even broader problem areas: designing group behaviour; designing institutions; the allocation of expert attention; amplifying collective intelligence; open science; scaling human systems; and artificial intelligence.
A broad question to return to: Why have the visions of Engelbart, Licklider, Kay et al mainly had an indirect (albeit enormous) impact on what people actually work on? The related communities and institutions and resources we have (in industry, academia, and elsewhere) are mostly organized around much smaller visions. That's really interesting. I have a vague sense of why this has happened, but I should distill a well thought out answer, not the bromides I've heard in the past.
Another broad question to return to: I've spoken informally of new representations, new operations, new fundamental objects, all without defining what those terms mean. Indeed, my useage of the terms has been somewhat inconsistent through the notes. Of course, it's counter-productive to fixate too early on questions of definition – all these concepts are, in some sense, emergent concepts that we are constructing out of the Turing soup, and it will take time to become clear what the right concepts are. But it may help achieve clarity to play a little with what these concepts mean, and how they relate.
A point of (possible) pessimism to analyse in more depth: a skeptic might say: "Well, it's all very well to do this kind of thing with simple things like difference equations and so on, but it'll never work for sophisticated exploration of [insert favourite highly abstract mathematical object here]". My own explorations suggest there's at least a grain of truth – the grain being that it will be quite a bit more difficult. However, one also naturally suspects that the real explanation is simply that we need to build up to it. We don't begin a student's education by defining Riemannian manifolds, geodesics, the Levi-Civita connection, etcetera. Instead, we begin with simpler concepts — $R^n$, vector fields, simple differential operators like $d / dx$, and so on, and gradually build up. I expect the same will be true of a "new interface" for mathematics. Still, it may be useful to dig into this in more depth.
To push further in the directions described here, I'd need to learn both to program well, and to design user interfaces well. Both these abilities seem to me to be super-powers, enlarging in a way similar to learning to write; it's well worth taking time to acquire at least a basic facility, and perhaps more. I found it challenging to build out even the very simple systems in these notes – the non-linear scrubbable numbers and the sine visualization. I learnt a lot. The combination to practice over and over is something like: identify a rough version of a design problem (like the problem of developing granular scrubbable numbers); sketch out an initial (really bad) idea for a solution; implement; criticise the problem and solution; iterate. Lots of practice will be needed, challenging myself frequently to step up to new levels! It's worth starting even with very simple problems. I did not anticipate how much I would learn from the granular scrubbable numbers problem, nor, indeed, how much I clearly still could learn from further iterations. Victor's essay Up and Down the Ladder of Abstraction shows the great depth even in a problem such as: how to drive a (very simple simulated) car down a (very simple simulated) road?
In these notes I've mentioned many elementary problems to return to in this vein, including: (1) Improving the granular slider (explore the momentum and damping idea, the memory idea, and the minimal change problem); and (2) Prototyping environments which would help a researcher discover the result about the representation of quantum states which I mentioned earlier.
More ambitious goals would be to develop interactive essays explaining the basic ideas of a subject such as quantum computing or neural networks. I've begun sketching out prototype interactive essays explaining the quantum gate model, quantum teleporation, and backpropagation. I've learnt a great deal from the sketches, and am encouraged, although it's also gradually becoming clear just how difficult it will be to do this well. Fortunately, it's also extremely motivating and exciting, and for that reason may be a better target than the more elementary problems.
Acknowledgements
Thanks to Jen Dodd and Ilya Grigorik for many conversations on topics related to these notes. And thanks to Jen Dodd for detailed feedback that greatly improved the notes.